Софийски университет „Св. Климент Охридски”

Факултет по математика и информатика

 

ДИПЛОМЕН  ПРОЕКТ

Тема: АЛГОРИТМИ. Същност, свойства и видове.

Основни понятия и програмиране на С#.

Web адрес: http://gogors.free.bg/

на: ГЕОРГИ РУДОЛФ САЧКОВ

Специализация: СДК Учител по Информатика и ИТ

Научен ръководител: доц. Ангел Ангелов

София 2018/2019 год.

Учебен предмет: Програмиране. Код: 4810201/17.

Клас: 9, 10         Професия: Системно програмиране.

 Специалност: Системен програмист.

Тип на училището: ПРОФЕСИОНАЛНА ГИМНАЗИЯ по ЕЛЕКТРОТЕХНИКА и АВТОМАТИКА.

Форма на обучение: Задължителна подготовка.

Модул: АЛГОРИТМИ.

Тема на учебната програма: Алгоритми – същност, свойства и видове. Основни понятия и програмиране на C#.

Технически и софтуерни условия, необходими за провеждане на обучението:

         А) Минимално необходими:

                   – Компютри: Intel Pentium 486; 1 GB RAM; 20 GB HDD;

                   – Операционна система – Windows XP;

                   – Google Chrome.

         Б) Реално съществуващи в училището:

                   – Компютри: Intel(R) Pentium(R); 2/4 GB RAM; 500 GB HDD

                   – Операционна система – Windows 7 и 10.

                   – Google Chrome

Дидактически материали, използвани в проекта:

1.     Ангелов А., Добрев Д., Хиков Т., Информатика 9 клас, Сиела – Софт енд Пъблишинг, София, 2002.

2.     Ангелов А.-Ачо, Ковачева Ел., Харизанов К., Сребрева Т., Информационни технологии 10 клас, Издателство „Булвест 2000“, 2018.

3.     Първанов Ив., Бонев Л., Информационни технологии 10 клас, Издателство „Домино“, Ст. Загора, 2019. http://Inftech.bgtest.eu

4.     Гъров К., Анева Ст., Тодорова Ел., Данаилов Д., Стоицов Г., Информационни технологии 10 клас, Издателство „Изкуства“, София, 2019. ПГДС - Уеб Портал с Електронни Учебници .

5.     Наков Св., Колев В и Колектив, Въведение в Програмирането със С#, Software University, София, 2015, http://www.introprogramming.info.

6.     Online C#: https://dotnetfiddle.net/ .

УРОК 1

ТЕМА : Алгоритми.

Вид на урока – комбиниран урок, в компютърен кабинет, продължителност 45 мин.

Опорни знания и умения

         Този урок е от нов раздел, като до този момент са учили Бройни системи и Булева алгебра и са придобити знания и учениците могат да работят с различните видове бройни системи да преобразуват числата от една бройна система в друга и да извършват на аритметични операции с числата. Учениците също вече са запознати с логическите функции (И, ИЛИ, НЕ) и са придобили умения за реализация и приложението им.

Въведени и усвоени  знания и умения, които имат отношение и ще бъдат използвани в урока:

·        Аритметични операции с числа в различните.

·        Основни логически операции и схеми И, ИЛИ, НЕ.

Ресурсни материали:

·        On line среда работа в Интернет среда с браузер.

Ø Цел на урока:

1.     Придобиване на общи познания за същността и свойствата на алгоритмите.

Учебно съдържание:

Понятия:

-         Алгоритъм определение, същност и свойства.

-         Начини за представяне на алгоритмите.

-         Web browser.

Умения за:

-         Познаване на основните алгоритми, същност, свойства.

-         Знания за съставяне на алгоритмите.

-         Реализация на знанията в съставяне на алгоритми в on line среда.

ПЛАН  НА  УРОКА:

Първите 30 минути използвам да дам ТЕСТ за упражнение, проверка и оценка на знанията и уменията на учениците как са овладели предходния материал за Бройни системи и Булева алгебра. За целта раздавам на всеки ученик четири подбрани въпроса от ТЕСТ-а по групи за самостоятелна работа:  (http://grs.free.bg/O6pa3oBaHue/TECT0.html). Следя работата на учениците и към края на 30-тата минута ги оценявам, като за всеки верен отговор по 1 т. Оценката се формира 2 + Точки.

 

ТЕСТ за Бройни системи и Булева алгебра.

1. Конюнкцията е:

а) просто съждение

б) съждение, получено от други съждения, свързани с логическа връзка ИЛИ

в) съждение, получено от други съждения, свързани с логическа връзка И

г) вярностна стойност на съждение

2. Дизюнкцията има вярностна стойност неистина когато:

а) едното съждение има вярностна стойност истина, а другото - неистина

б) и двете съждения имат вярностна стойност истина

в) и двете съждения имат вярностна стойност неистина

г) друг отговор

3. Каква е логическата операция в израза: "Огря слънце и изсуши росата."

а) конюнкция

б) дизюнкция

в) импликация

г) отрицание

4. Дадени са твърденията: p: Не учих по програмиране. q: Издържах теста. Кой от логическите изрази съответства на словесния израз: "Не учих по програмиране и издържах теста."

а) p Λ ¬ q

б) p Λ q      

в) ¬p Λ q

г) p v ¬ q

5. Дадени са следните твърдения: p: Днес валя дъжд. q: Видяхме дъгата. Кое твърдение съответства на логическия израз p Λ ¬q

а) Днес валя дъжд и видяхме дъгата

б) Днес не валя дъжд и не видяхме дъгата

в) Днес не валя дъжд и видяхме дъгата

г) Днес валя дъжд и не видяхме дъгата

6. Пресметнете стойността на булевия израз (¬а Λ (¬b v c)) v (c Λ b) при а=0,b=0,c=1

а) 1

б) 0

в) не знам

г) не е възможно

7. Проверете еквивалентни ли са изразите ¬ (p v q) и p Λ ¬q

а) не

б) да

в) не знам може би

г) друг отговор

8. Намерете вярностната стойност на израза   ¬p Λ¬(q v p) за р=1 и q=0

а) 1

б) 0

в) не е възможно да се пресметне

г) не знам

9. Кой от следните изрази е еквивалентен на израза: ¬(x v у) Λ ¬(x Λ (x v 0))

а) ¬x v у

б) x v у

в) ¬ x Λ ¬у

г) x Λ ¬  у

10. Изразът ¬(p Λ ¬q) е еквивалентен на израза:

а) p v q

б) p Λ q

в) ¬p v  q

г) p v ¬q

11. Изразът: (¬ (1 Λ c) Λ c) v ¬(0 Λ ¬c) e равен на:

а) ¬x v у

б) 0

в) 1

г) x Λ ¬  у

12. Коя от следните стойности е еквивалентна на израза ¬(1 v ¬ k)Λ(1 v ¬(¬k v 1))

а) 0

б) ¬k

в) k

г) 1

13. Десетичното представяне на числото 110011(2)е:

а) 51

б) 52

в) 50

г) 17

14. Двоичното представяне на числото 17(10) е:

а) 10001

б) 11000

в) 10010

г) 11111

15. Числото 13D(16) записано в двоичната бройна система е:

а) 100001101

б) 100000000

в) 100111101

г) 111001100

16. Числото 101101111(2), записано в шестнадесетична бройна система е:

а) 16F

б) 16B

в)  13A

г)  друг отговор

17. Числото 15(10) записано в осмична бройна система е:

а) 17

б) 10

в) 13

г)  FF

18. Числото 12(8) записано в десетичната бройна система е:

а) 17

б) 60

в) 10

г) 7

19. Числото А4(16) записано в десетичната бройна система е:

а) 164

б) 160

в) 168

г) друг отговор

20. Числото 154(8) записано в бройна система с основа 16 е:

а) 6C

б) 128

в) 43

г) 21033

21. Сумата на числата 1100111(2) и 111010(2) е:

а) 101001001

б) 101101000

в) 10100001

г) 11111110

22. 110001001(2) - 111011(2) е:

а) 1001010101

б) 1100010110

в) 101001110

г) 1010110

23. Произведението на числата 101101(2) и 1011(2) е:

а) 101010101

б) 111101111

в) 101010111

г) 110011001

24. Двоичната бройна система е позиционна бройна система.

а) вярно

б) грешно

в) не знам

г) друг отговор

25. В един байт е записано числото 11(10). Колко е броят на двоичните единици в байта?

а) 3

б) 5

в) 2

г) 7

 

ТЕСТ-а без отговори: http://grs.free.bg/O6pa3oBaHue/TECT25--.html

ТЕСТ-а с отговори: http://grs.free.bg/O6pa3oBaHue/TECT25++.html

Успоредно с това следя работата на учениците и справянето им с ТЕСТ-а. Специално наблюдавам кой от въпросите затруднява учениците, като избирам конкретен ученик който се е справил с решаването на задачата предизвикала затруднения, като карам този ученик да представи решение и го обсъждаме всички заедно. Ако няма кой да представи решение в достатъчна разбираема степен аз коментирам и представям решение.

В останалите 15 минути от часа за мотивиране, въвеждане и усвояване на новото учебно съдържание относно АЛГОРИТМИ използвам демонстрационна алгоритмична игра задача WEB on line:

ЗАДАЧА:

Селянин трябва да превози през река вълк, коза и зелка. Но лодката е такава, че в нея може да се побере селянинът, а освен него или само вълкът, или само козата, или само зелката. Ако остави на брега вълка сам с козата, козата ще бъде изядена, а ако остави козата сама със зелката, козата ще изяде зелката.

Съставете алгоритъм как селянинът да прекара товара си цял и непокътнат?

http://abc-bg.be/river.html или

https://www.vgames.bg/igra/logicheski-igri/238/valk-ovca-i-zele;

Разяснявам задачата и правя анализ на първичните данни и зависимости. Коментирам начините за решение в резултат на което предлага стратегия за избора на решението.

До края на часа учениците решават следните задачи самостоятелно или като се консултират и по между си, като учителят следи, подпомага и направлява учениците:

ЗАДАЧА:

Имате 9 монети, едната от които е фалшива (тя е по-тежка). Имате везна. Съставете и опишете алгоритъм, като с най-много две измервания откриете фалшивата монета.

ВИЗУАЛНО РЕШЕНИЕ:

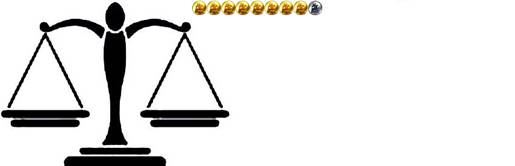
В рамките на няколко минути обобщавам решението:

Разделяме 9-те монети на 3 х 3.

Поставяме 6 монети, като ги поставяме 3 на 3 (остават 3):

а) везната не се отклонява:

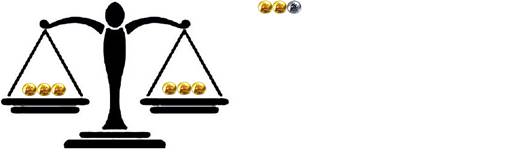
Фалшивата монета е при 3те монети които не са на везната.

б) везната се отклонява:

Фалшивата монета е при 3те монети които са по-тежки на везната.

Варианти при 1-во измерване:

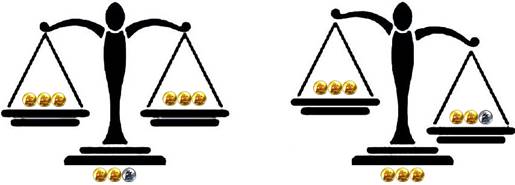
Варианти при 2-во измерване:

а) везната не се отклонява:

Фалшивата монета не е на везната.

б) везната се отклонява:

Фалшивата монета е по-тежката на везната.

Видео решение: https://youtu.be/5Qh6kagyhHg

 

Давам за домашно следната задача:

ЗАДАЧА:

Имате 17 монети, едната от които е фалшива (тя е по-лека). Имате везна. Съставете и опишете алгоритъм, като с най-много три измервания откриете фалшивата монета.

УРОК 2

ТЕМА : Алгоритми  – същност, видове.

Вид на урока – комбиниран урок, в компютърен кабинет, продължителност 45 мин.

Опорни знания и умения

         До този урок са въведени и усвоени следните знания и умения, които имат отношение и ще бъдат използвани в урока:

·        Същност и видове алгоритми.

·        Работа в Интернет среда с браузер.

Ресурсни материали:

Ø On line среда WEB browser

Цел на урока:

1.)  Упражняване съставяне на алгоритми.

2.)  Упражняване съставяне различни видове блокови схеми на алгоритмите.

Учебно съдържание:

Понятия:

-         Алгоритъм и начини за представяне на алгоритмите.

Умения за:

-         Познаване на основните алгоритми, същност, свойства.

-         Знания за съставяне на алгоритмите.

ПЛАН  НА  УРОКА:

Първите 10 минути проверявам и коментирам задачата от домашното на миналия урок, като представям видео решение:

https://youtu.be/En8iDuFQC78

Поставям нова задача и през следващите 10 минути решаваме следната:

ЗАДАЧА:

Баща и двамата му сина трябва да преминат през река. Намерили лодка, която издържа товар до 120 кг. Бащата е 100 кг., син1 е 50 кг., а син2 е 60 кг. Да се състави алгоритъм за преминаване на реката от тримата!

 

Дадено:      Баща(Б)=100 ; син1(С1)=50 ; син2(С2)=60 ; Лодка(Л)=0 ;

Ляв Бряг (ЛБ) = Б + С1 + С2 = 100+50+60=210 ; Десен Бряг (ДБ)=0.

ТАБЛИЧНО РЕШЕНИЕ с ФОРМУЛИ:

в лодката ще качваме спазвайки  условието до 120 кг. товар:

ФОРМУЛИ

коментар

Ляв

Бряг

(ЛБ)

Лодка

(Л)

Десен

Бряг

(ДБ)

Б=100 ; C1=50 ; С2=60 ; Л=0 ; ЛБ=0

Дадено

Б,С1,С2

0

0

ДБ=Б+С1+С2 ; Л=0 ; ЛБ=0

Начално състояние

Б,С1,С2

0

0

ДБ=ДБ-С1-С2 ; Л=Л+С1+С2 ; ЛБ=0

в Лодката са С1 + С2

Б

С1,С2

0

ДБ=ДБ ; Л=Л-С1 ; ЛБ=ЛБ+С1

С1 слиза на ДБ;С2

Б

С2

С1

ДБ=ДБ+С2 ; Л=Л+Б-С2 ; ЛБ=ЛБ

С2 и Б се разменят

С2

Б

С1

ДБ=ДБ ; Л=Л-Б+С1 ; ЛБ=ЛБ+Б-С1

С1 и Б се разменят

С2

С1

Б

ДБ=ДБ-С2 ; Л=Л+С2 ; ЛБ=ЛБ

в Лодката са С1 + С2

0

С1,С2

Б

ДБ=0 ; Л=Л-С1-С2 ; ЛБ=ЛБ+С1+С2

С1 и С2 слизат на ДБ

0

0

Б,С1,С2

 

ГРАФИЧНО РЕШЕНИЕ:

 

ВИДЕО РЕШЕНИЕ: https://youtu.be/PSDrvDIHw0s

В следващите 25 минути представям основни свойства понятия и видове:

АЛГОРИТЪМИ – това е последователност от действия(стъпки) върху входни данни, които след изпълнението си дават резултат и приключват за крайно време. Компютърните алгоритми притежават следните свойства:

§  Определеност (детерминираност) – алгоритъмът може да се изпълни многократно, като за едни и същи начални-входни данни се  получават едни и същи изходни резултати независимо от изпълнителя

§  Масовост – алгоритъмът трябва да е приложим не за една задача, а за цял клас еднотипни задачи.

§  Крайност и Резултатност – алгоритъмът се изпълнява за краен брой стъпки и дава краен конкретен резултат.

§  Дискретност – алгоритъмът се състои от краен брой действия, като след дадено действие се преминава към точно определено следващо.

§  Формалност – позволява изпълнение от автомат/машина.

§  Сложност (ефективност) – е анализ и е свързан с броя операции, а ефективността е използваните ресурси (памет, изчислителна мощ).

Начини за представяне на алгоритмите:

§  Словесно – чрез използване на човешки език.

§  Графично – последователност от фигури (картинки, рисунки) .

§  Схематично – блок схема, като се използват следните обозначения:

o   Начало –

o   Край –

o   Вход/Изход –   

o   Блок за обработка (функционален) –

o   Условие (логически блок) – if

o   For цикъл –

§  Език за програмиране С# – компютърен (машинен).

В оставащите минути до края на часа давам за решение следната:

ЗАДАЧА:

Съставете алгоритъм за размяна съдържанието на две чаши А-вино и В-сок.

Използваме трета празна чаша, като имаме следните стъпки:

1). Начало: А-вино , В-сок , С-празна

2). Преливаме в празната чаша C сока от чаша В, в резултат на което става: чаша В става празна, а чаша С със сок.

3). Преливаме в празната чаша В виното от чаша А, в резултат на което става: чаша А става празна, а чаша В със вино.

4). Преливаме в празната чаша А сока от чаша С, в резултат на което става: чаша С става празна, а чаша А със сок.

При което разменихме съдържанието на две чаши А и В и в резултат на което стана чаша А-сок , чаша В-вино.

ГРАФИЧНО РЕШЕНИЕ:

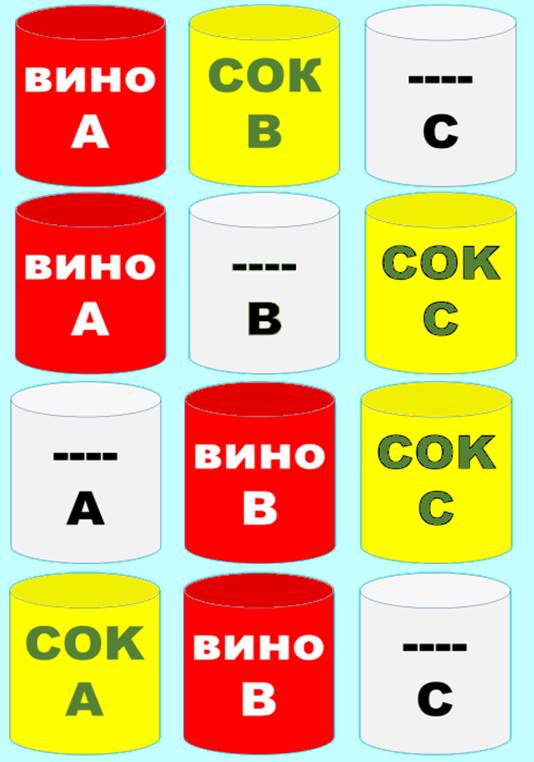
УРОК 3

 

ТЕМА : Алгоритми  – графично представяне

.

Вид на урока – комбиниран урок, в компютърен кабинет, продължителност 45 мин.

Опорни знания и умения

         До този урок са въведени и усвоени следните знания и умения, които имат отношение и ще бъдат използвани в урока:

·        Същност и видове алгоритми.

·        Работа в Интернет среда с браузер.

Ресурсни материали:

Ø On line среда WEB browser

Цел на урока:

1.)  Упражняване съставяне на графични алгоритми.

2.)  Упражняване съставяне различни видове схеми на алгоритмите.

Учебно съдържание:

Понятия:

-         Алгоритъм и графични начини за представяне на алгоритмите.

Умения за:

-         Познаване на основните графични алгоритми.

-         Знания за съставяне на графичните алгоритмите.

 

ПЛАН  НА  УРОКА:

Първите 10 минути поставям нова задача:

ЗАДАЧА:

На плавателен канал се срещат два конвоя кораби. Каналът има разширение, в което може да се побере само един кораб. Съставете графичен алгоритъм как да се разминат двата конвоя кораби, като всеки продължи в своята посока.

ГРАФИЧНО РЕШЕНИЕ:

ВИДЕО РЕШЕНИЕ: https://youtu.be/TSlRbgaxSrw

През следващите 10 минути решаваме следната:

ЗАДАЧА:

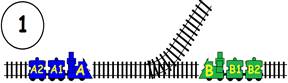
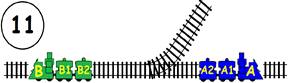
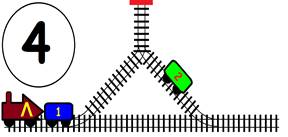
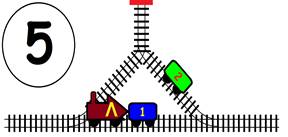
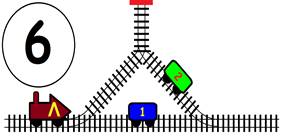
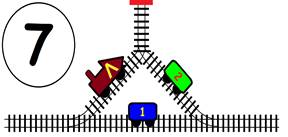
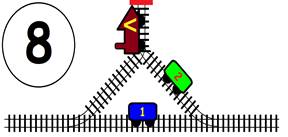
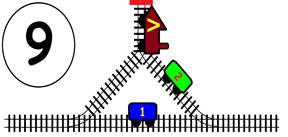
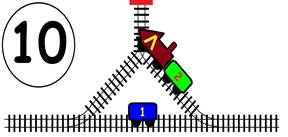
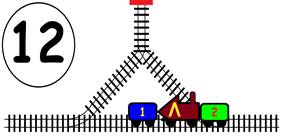
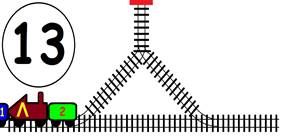
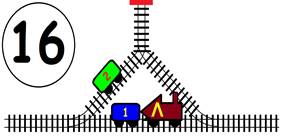
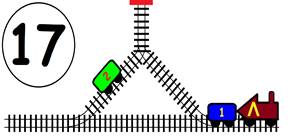
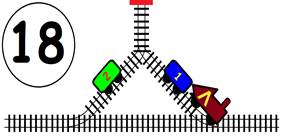
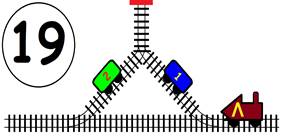
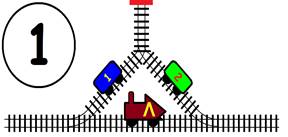
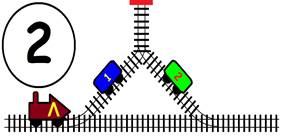
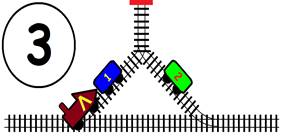
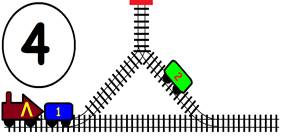
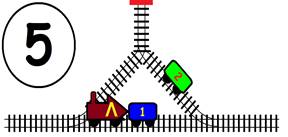
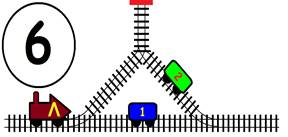
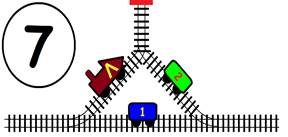
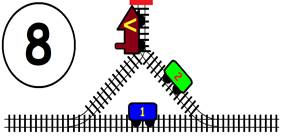
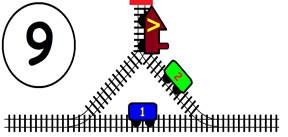
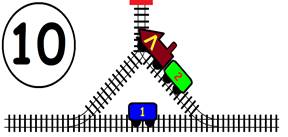
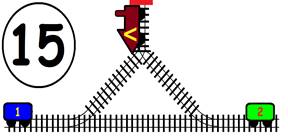
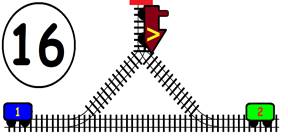
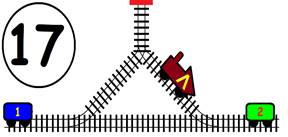
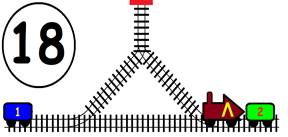
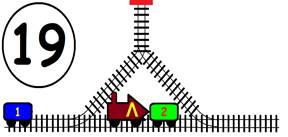
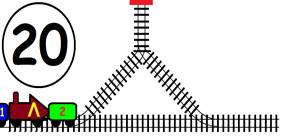
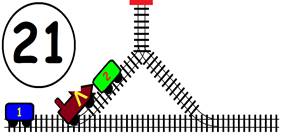
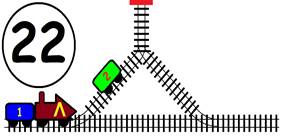
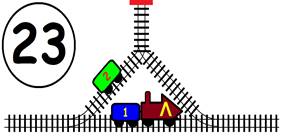
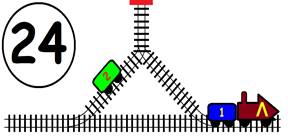
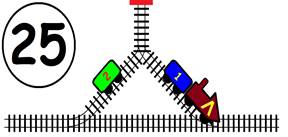
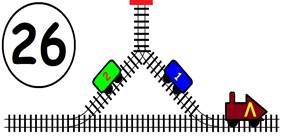
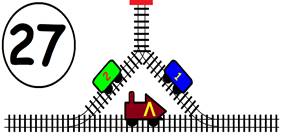
Срещат се две влакови композиции. Да се състави графичен алгоритъм.

Как ще се разминат, при наличието на глухо отклонение, което побира само един локомотив и един вагон?

ГРАФИЧНО РЕШЕНИЕ:

ВИДЕО РЕШЕНИЕ: https://youtu.be/TSlRbgaxSrw

В оставащите 25 минути решаваме следната:

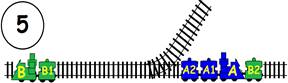
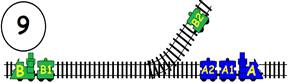
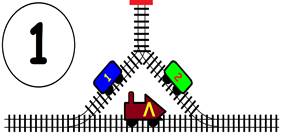
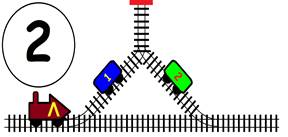
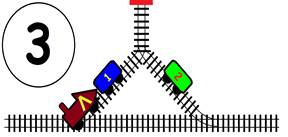
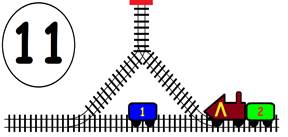
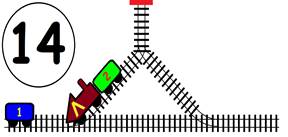
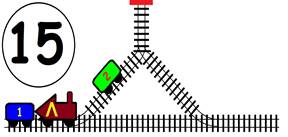
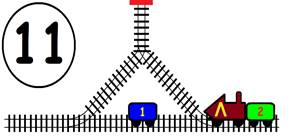
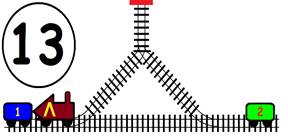
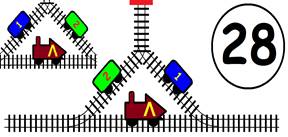
ЗАДАЧА:

На главна Ж.П. линия с две отклонения, като във всяко има по един вагон. В глухата линия може да влезе само един вагон или локомотив. Какви маневри трябва да извърши машинистът, за да размести вагоните, като им размени местата, а локомотивът да се върне в изходно положение (старото си място):

1). Обърнат в противоположна посока;

2). Запазвайки изходна посока. 

ГРАФИЧНО РЕШЕНИЕ на 1 – обърнат в противоположна посока  :

 

ВИДЕО РЕШЕНИЕ: https://youtu.be/8m9I2Ma4M48

 

ГРАФИЧНО РЕШЕНИЕ на 2 – локомотивът запазва изходната си посока:

ВИДЕО РЕШЕНИЕ: https://youtu.be/FS-nJrVnNac

 

УРОК 4

 

ТЕМА : Алгоритми  – Начини на описание. Блок схеми.

Вид на урока – комбиниран урок, в компютърен кабинет, продължителност 45 мин.

Опорни знания и умения

         До този урок са въведени и усвоени следните знания и умения, които имат отношение и ще бъдат използвани в урока:

·        Същност и видове алгоритми.

·        Работа в Интернет среда с браузер.

Ресурсни материали:

Ø On line среда WEB browser

Цел на урока:

1.)  Упражняване съставяне на блок-схема на алгоритми.

2.)  Упражняване съставяне различни видове схеми на алгоритмите.

Учебно съдържание:

Понятия:

-         Алгоритми и блокови схеми за представяне на алгоритмите.

Умения за:

-         Познаване на основните блокови схеми за алгоритми.

-         Знания за съставяне на блокови схеми за алгоритмите.

ПЛАН  НА  УРОКА:

Първите 10 минути представям и коментираме блок схеми на различни видове алгоритми:

i.       Линеен – последователни действия в едно направление. …

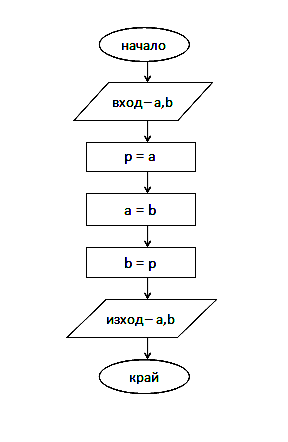
ii.     Разклонен – съществува условен логически блок

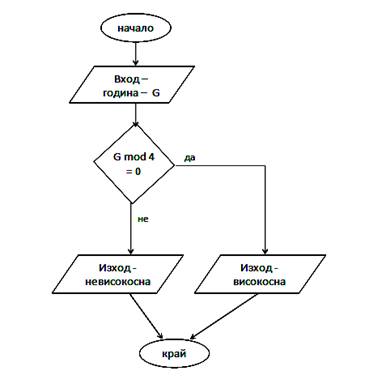
През следващите 10 минути решаваме разклонен алгоритъм и следната:

ЗАДАЧА:

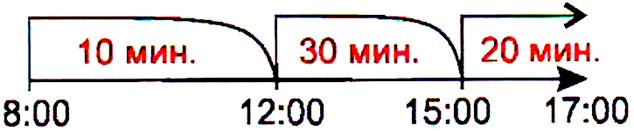
Иванчо и Марийка работят във фирма с работно време от 8:00 до 17:00 часа, с право на почивка веднъж на ден в кръгъл час (h), като продължителността на почивката се определя от следните правила:

         Ако h < 15:00

                   Ако h < 12:00

                            10 минути

                   Иначе

                            30 минути

         Иначе

                   20 минути

         Иванчо почива от 13:00, а Марийка от 15:00. По колко минути почива Иванчо и Марийка?

РЕШЕНИЕ:

В алгоритъма, има две условни конструкции. Контролните точки са две: в 12:00 и в 15:00 часа.

В първата условна конструкция, при h < 15:00, е вложена втора условна конструкция Ако h < 12:00 … Иначе … . Следователно до втората условна конструкция може да се стигне, Ако h < 15:00.

В случая е представен разклонен алгоритъм и заместваме:

1.)  h = 13.

2.)  Тъй като 13 < 15, ще се изпълни разклонението, съдържащо ново условие Ако h < 12:00.

3.)  Тъй като 13 е по-малко от 12, ще се изпълни алтернативното условие, описано след Иначе, т.е. Иванчо почива 30 минути.

4.)   h = 15, ; 15 не е по-малко от 15. Следователно се прескача цялата конструкция Ако h < 12:00 … Иначе … и се преминава към второто Иначе …

5.)  Следователно почивката на Марийка е 20 минути.

Представяне решението на

В оставащите 25 минути до края на часа представям:

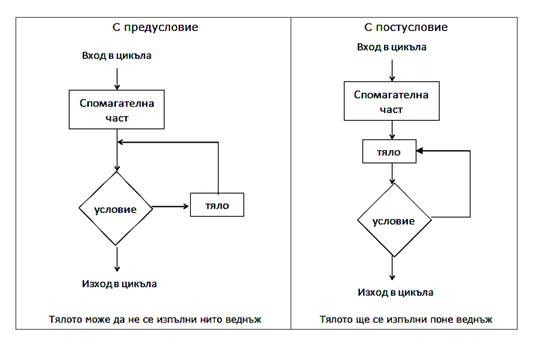
iii.  Циклични – повтарящи се действие/я в зависимост от дадено условие има следния състав: тяло, условие, начало, стъпка, край.

·  Пред–условие

·  Пост–условие

 

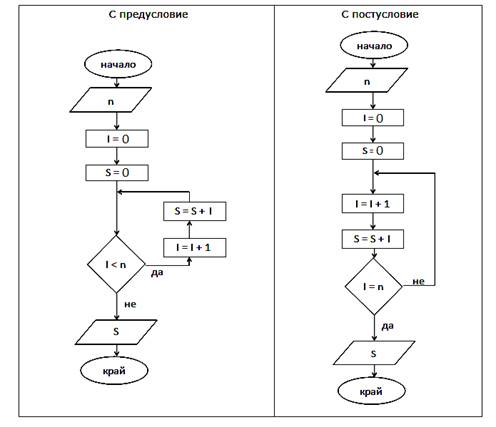
Пример:

Блок схема  Цикличен алгоритъм на Евклид за НОД:

 

 

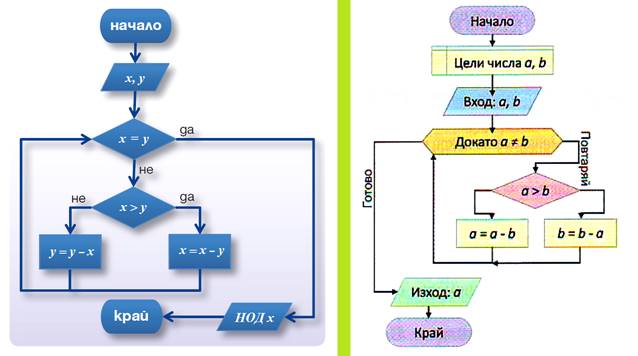
УРОК 5

 

ТЕМА : Алгоритми  сортиране.

Вид на урока – комбиниран урок, в компютърен кабинет, продължителност 45 мин.

Опорни знания и умения

         До този урок са въведени и усвоени следните знания и умения, които имат отношение и ще бъдат използвани в урока:

·        Същност и видове алгоритми за сортиране.

·        Работа в Интернет среда с браузер.

Ресурсни материали:

Ø On line среда WEB browser

Цел на урока:

1.)  Съставяне на алгоритми за сортиране.

2.)  Упражняване съставяне различни видове на алгоритми за сортиране.

Учебно съдържание:

Понятия:

-         Представяне на алгоритми за сортиране.

Умения за:

-         Познаване на основните алгоритми за сортиране.

-         Знания за съставяне на алгоритмите за сортиране.

ПЛАН  НА  УРОКА:

Първите 15 минути представям и коментираме блок схеми на различни видове АЛГОРИТМИ ЗА СОРТИРАНЕ:

Видове: Известни са стотици методи (алгоритми) за сортиране които подреждат елементите на място (без да се използва помощен масив, което е доста неефективно от гледна точка на заеманата памет), но всеки един от тях може да се отнесе към една от три основни групи, а именно методи за сортиране чрез:

     1. Сортиране чрез размяна:

         • метод на мехурчетата (пряка размяна);

         • метод на шейкър сортиране (“чрез клатене”);

         • метод на бърза сортировка на Hoare.

     2. Сортиране чрез селекция (избор):

         • метод на пряка селекция;

         • метод на пирамидална сортировка.

     3. Сортиране чрез вмъкване:

         •   метод на пряко вмъкване;

         •   метод на двоично вмъкване;

         •   метод на вмъкване с намаляваща стъпка.

ИДЕЯ на метода:

Масивът се обхожда n-1 пъти, като на стъпката (обхождането)

с номер i се избира най-големият измежду първите n-i+1 елемента и той се поставя на n-i+1 -во място в масива.

Словесно описание на алгоритъма - 1:

    1. i = 1 (i – номер на стъпка)

    2. Между елементите от a[1] до a[n-i+1] търсим максимален елемент. Нека той е a[k].

    3. Елементът a[k] разменя мястото си с елемента a[n-i+1]

    4. i = i + 1;   проверяваме дали i < n,

ако ДА се преминава към т. 2,

ако НЕ се преминава към т. 5.

    5. Край

Метод на СОРТИТАНЕ с ПРЯКА СЕЛЕКЦИЯ

Би могло да се избира най-малкият елемент и съответно – да се поставя на такова място в началото на масива, че масивът да се сортира възходящо. В този случай се ползва следната технология:

Словесно описание на алгоритъма - 2:

     1. i = 1 (i – номер на стъпка)

     2. Между елементите от a[i-1] до a[n-1] търсим минимален елемент. Нека той е a[k].

     3. Елементът a[k] разменя мястото си с елемента a[i-1]

     4. i = i + 1;   проверяваме дали i < n,

ако ДА се преминава към т. 2,

ако НЕ се преминава към т. 5.

     5. Край

Оценка на бързодействието на алгоритъма

При изпълнението на алгоритъма за сортиране чрез пряка селекция се извършват :

   • n-1 сравнения при определяне на първия най-малък елемент (n е размерност на списъка или едномерния масив);

   • n-2 сравнения при определяне на втория най-малък елемент;

   • n-3 - за третия и т.н.

Общият обем на сравненията за такъв алгоритъм се определя по формулата:

(n-1) + (n-2) + (n-3) + ……. + 4 + 3 + 2 + 1 = (n2-n)/2 = n*((n-1)/2),

където (n-1)/2 е средният брой сравнения за 1 итерация на външния цикъл. Сложността в терминологията на О-нотацията е О(n2). В този вариант на сортиране броя на сравненията не зависи от техния начален порядък.

 

1.  Сортиране чрез вмъкване

Списъкът с елементи, които ще бъдат сортирани се разделя на две части: частта със сортираните елементи и частта с несортираните

1.  При всяка стъпка се взема първия елемент от несортирания списък и се вмъква на правилната позиция в сортираната част от списъка

2.  Сортирането продължава докато елементите от несортираната част на списъка се изчерпят.

Пример:

   

46

60

56

81

16

Взема се първия елемент от несортирания списък (46) и се поставя на правилното място в сортирания.

46

60

56

81

16

Взема се първия елемент от несортирания списък (60) и се поставя на правилното място в сортирания.

46

60

56

81

16

Взема се първия елемент от несортирания списък (56) и се поставя на правилното място в сортирания.

46

56

60

81

16

Взема се първия елемент от несортирания списък (81) и се поставя на правилното място в сортирания.

46

56

60

81

16

Взема се първия елемент от несортирания списък (16) и се поставя на правилното място в сортирания.

16

46

56

60

81

Списъкът е сортиран

 

Следващите 15 минути представям

 

2. Сортиране на масив по метода на пряката селекция.

Сортирането във възходящ ред (от малка към голяма стойност) може да се опише със следния алгоритъм:

1)    намира се най-малкият елемент на масива;

2)    той си разменя мястото с първият елемент на масива.

Така на първо място е отсят най-малкият елемент от масива. Тази операция се повтаря с останалите n-1 елемента, а след това с останалите n-2 елемента и т.н., докато остане само един елемент – най-големият.

Пример:

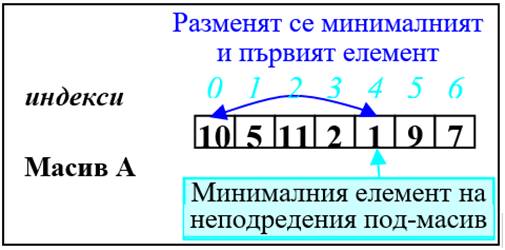
Да се подреди в низходящ ред масива A[4]={10,5,11,2,1,9,7}

Променливата i следи началото на неподредения под-масив.

1.  Целият масив е неподреден  i =0.

a)       Намира се минималният елемент на масива - A[4]=1.

b)      Първият елемент на неподредения под-масив (A[0]) и минималният (A[4]) разменят местата си.

Първият елемент вече е на мястото си.

 

2.  Неподреденият под-масив започва от втория елемент (i =1).

a)       Намира се минималния елемент на неподредения под-масив - A[3]=9.

b)      Първият елемент на неподредения под-масив (A[1]) и минималния (A[3]) разменят местата си.

И вторият елемент вече е на мястото си.

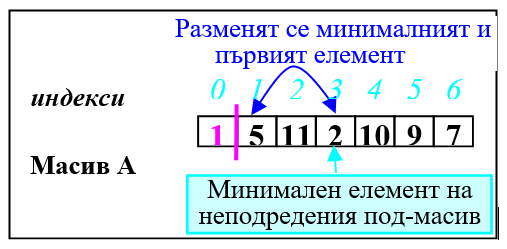
3.  Неподреденият под-масив започва от третия елемент (i =2).

a)       Намира се минималния елемент на неподредения под-масив - A[3]=7.

b)      Първият елемент на неподредения под-масив (A[2]) и минималния (A[3]) разменят местата си.

И третият елемент вече е на мястото си.

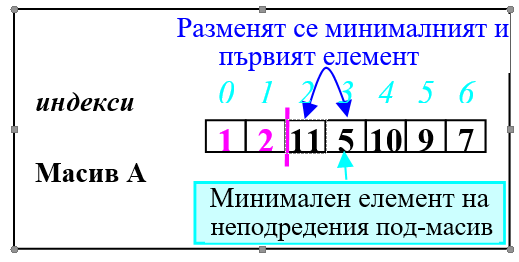
4.  Неподреденият под-масив започва от четвъртия елемент (i =3).

a)       Намира се минималния елемент на неподредения под-масив - A[6]=5.

b)      Първият елемент на неподредения под-масив (A[3]) и минималния (A[6]) разменят местата си.

И четвъртият елемент вече е на мястото си.

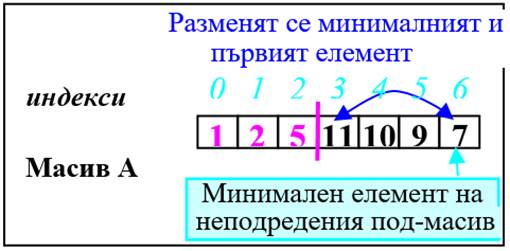
5.  Неподреденият под-масив започва от петия елемент (i =4).

a)       Намира се минималния елемент на неподредения под-масив - A[5]=2.

b)      Първият елемент на неподредения под-масив (A[4]) и минималния (A[5]) разменят местата си.

И петият елемент вече е на мястото си.

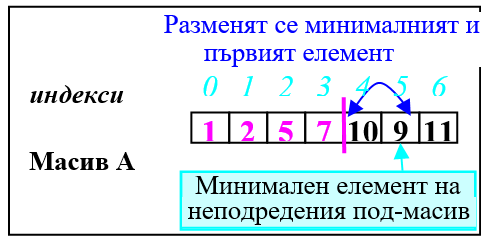
6.  Неподреденият под-масив започва от шестия елемент (i =5).

a)       Намира се минималния елемент на неподредения под-масив - A[5]=1. Той е и първия елемент на неподредения под масив и размяна не се налага. Но за да се спази принципа се прави размяна на елемента със самия себе си.

b)      Първият елемент на неподредения под-масив (A[5]) и минималния (A[5]) разменят местата си.

И шестият елемент вече е на мястото си.

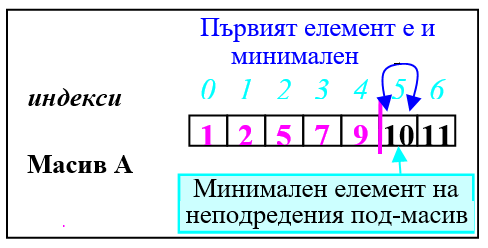
7.  Неподреденият под масив започва от седмия елемент (i =6), които е и последния елемент на масива. След като всички останали елементи са си на мястото, следва, че и този елемент си е на мястото и масивът е подреден в възходящо ред.

 

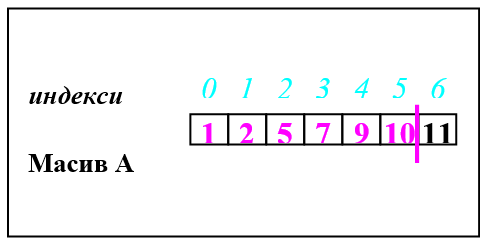
За програмната реализация на този метод е необходимо да се организират два цикъла. Във вътрешния цикъл се намира минималният елемент на неподредения под масив и неговия индекс. Външен цикъл, в който се следи началото на неподредения под масив и се извършва размяната на първия и минималния елемент на неподредения под масив. Вътрешния цикъл се изпълнява за стойности на индексната променлива j от i  до n-1 (последния елемент на масива). Външния цикъл се изпълнява за стойности на индексната променлива i от 1 до n-2 (предпоследния елемент на масива).

 

В оставащите 25 минути до края на часа представям:

 

3. Описание на quicksort (Сортиране по дялове – бързо сортиране)

Като се има предвид, че метода на мехурчето(пряката размяна) е най-неефективният метод за сортиране трябва да се очаква сравнително голям процент на подобрение. Изненадващо обаче е, че подобрението на този метод води до най-добрият метод за сортиране на масиви, познат до сега. Неговата ефективност е толкова голяма, че авторът му C.A.R.Hoare го е нарекъл бързо сортиране.

Бързото сортиране се основава на факта, че на колкото по-големи разстояния се правят разместванията, толкова по-ефективно е сортирането.

 Нека е даден масив с n елемента, подредени по низходящ ред. Те могат да се сортират само с n/2 размени, като най-напред се разменят най-левият и най-десният елемент и постепенно се отива навътре и от двете страни.

 

 

Пример

масив А[10]                            281  163  87   71   58   21  12   8    5       0

подредения масив  A[10]       0       5      8    12   21   58  71   87  163  281

Естествено това се получава само ако масивът е обратно подреден, но можем да опишем нещо подобно и за неподреден масив:

1)    нека изберем един елемент от масива и го наречем х.

2)    сканираме масива отляво, докато намерим елемент, чиято стойност е по-голяма от х (ai > x).

3)    сканираме масива отдясно, докато намерим елемент, чиято стойност е по-малка от х (aj < x).

4)    разменяме стойностите на ai и aj.

5)    продължаваме стъпки 2, 3 и 4 дотогава, докато двете сканирания се срещнат някъде по средата на масива.

 

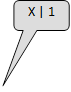X | 1Пример

 

 

i=0

1

2

3

4

5

6

7

8

j=9

86

35

72

42

94

56

18

67

22

5

 

 

 

i=2

 

 

 

 

 

j=8

 

5

35

72

42

94

56

18

67

22

86

 

 

 

 

 

 

i=4

 

j=6

 

 

 

5

35

22

42

94

56

18

67

72

86

 

Така получаваме два под-масива:

1)                     със стойности a[k] <= x и индекси k=0……(i-1);

2)                     със стойности a[k] >= x и индекси k=(j+1)……(n-1).

Всеки от двата под-масива се подрежда по същия начин. Получават се четири под-масива, които от своя страна също се подреждат по показания вече начин. Процедурата се изпълнява, докато си достигне до под-масиви, състоящи се от по един елемент.

 


0

1

2

3

4

5

6

7

8

9

 

5

35

22

42

18

56

94

67

72

86

 

 

х

 

 

 

 

х

 

 

 

0

1

2

3

4

5

6

7

8

9

 

5

18

22

42

35

56

67

94

72

86

х

 

 

х

 

х

 

 

х

 

 

0

1

2

3

4

5

6

7

8

9

 

5

18

22

35

42

56

67

72

94

86

 

 

 

х

 

 

 

 

х

 

 

 

0

1

2

3

4

5

6

7

8

9

5

18

22

35

42

56

67

72

86

94

 

Понякога двата под-масива могат да включват общи елементи (когато в масива има няколко елемента със стойност х). Тази област е a[k] = x  с индекси k=(j+1)……(i-1).

Web пример: https://bg.wikipedia.org/wiki/%D0%91%D1%8A%D1%80%D0%B7%D0%BE_%D1%81%D0%BE%D1%80%D1%82%D0%B8%D1%80%D0%B0%D0%BD%D0%B5#/media/%D0%A4%D0%B0%D0%B9%D0%BB:Sorting_quicksort_anim.gif

Пример:

 


i=0

1

2

 

3

4

5

6

7

j=8

9

2

5

 

8

2

6

2

1

0

 

 


0

i=1

2

3

4

5

6

j=7

8

0

2

5

8

2

6

2

1

9

 

 


0

1

i=2

3

4

5

j=6

7

8

0

1

5

8

2

6

2

2

9

0

1

2

i=3

j=4

5

6

7

8

0

1

2

8

2

6

5

2

9

 

0

1

2

j=3

i=4

5

6

7

8

0

1

2

2

8

6

5

2

9

 

0

j=1

2

3

i=4

5

6

7

8

0

1

2

2

8

6

5

2

9

Левият под-масив включва елементите с индекси от 0 до 3 (i-1), а десният- елементите с индекси от 2(j+1) до 8 (n-1 ).

С право възниква въпросът не може ли стойностите равни на х да не ги местим, т.е. уравнението a[i]<x да стане a[i]<=x и съответно a[j]>x да стане  a[j]>=x. Принципно е възможно, но крие опасност от излизане извън границите на масива.

Пример:

0

i=1

2

3

4

5

6

7

8

 

2

3

2

8

2

6

5

2

9

x=a[4]=2

Индексът i стартира от 0 и се увеличава докато a[i]<=x и когато се достигне до стойност a[i] >x спира (в случая i=1).

Индексът j стартира от 8 (n-1 ) и се намалява, докато a[j]>=x, но в случая всички елементи са >=2 и няма ограничение, което да спре индекса да не излезе извън границите на масива.

4. Метод на мехурчето (Bubblesort)

Алгоритъмът сравнява последователно всички двойки съседни елементи ai-1 и аi, и ако ai-1>ai местата им биват разменени. Методът може да се използва в програми, които трябва да подредят масив по даден критерий. a1 a3 a5 a2 a4 => a1 a2 a3 a4 a5.

Пример:

Ако несортираният масив има вид: 5 1 4 2 8 и искаме да получим елементите, сортирани във възходящ ред:

Вземат се първите два елемента от масива: 5 и 1

Тъй като 1 < 5 се разменят местата им. Текущ масив: 1 5 4 2 8

Вземат се следващите два елемента от масива: 5 и 4

Тъй като 4 < 5 се разменят местата им. Текущ масив: 1 4 5 2 8

Вземат се следващите два елемента от масива: 5 и 2

Тъй като 2 < 5 се разменят местата им. Текущ масив: 1 4 2 5 8

Вземат се следващите два елемента от масива: 5 и 8

Тъй като 5 < 8 не се извършва размяна. Тук спира първото обхождане на масива.

 

УРОК 6

 

ТЕМА : С# въведение и основи. Представяне линейни и условни (разклонени) алгоритми на С#.

 

Вид на урока – комбиниран урок, в компютърен кабинет, продължителност 45 мин.

Опорни знания и умения

         В този урок са въведени и усвоени следните знания и умения, които имат отношение и ще бъдат използвани в урока:

·        Същност и видове алгоритми.

·        Съставяне различни видове блокови схеми на алгоритмите.

·        Представяне сорс код на С# в on line среда на интернет за въвеждане и извеждане на информация за линейни и условни (разклонени) алгоритми.

·        Съхраняване на данни в email и извеждането им.

·        Работа в Интернет среда с браузер.

Ресурсни материали:

Ø On line среда на C# : https://dotnetfiddle.net/

Цел на урока:

1.)  Упражняване съставяне на различни видове алгоритми.

2.)  Упражняване съставяне различни видове блокови схеми на алгоритмите.

3.)  Упражняване за съставяне на сорс код на С# в on line среда на интернет на линейни и условни (разклонени) алгоритми.

Учебно съдържание:

Понятия:

-         Алгоритъм и начини за представяне на алгоритмите.

-         Ключови думи, Категории оператори и приоритет.

-         Типове данни на променливи.

-         Условен оператор If.

-         On line C#, Web browser, сорс код.

Умения за:

-         Познаване на основните алгоритми, същност, свойства.

-         Знания за съставяне на алгоритмите.

-         Реализация на знанията в съставяне на програма на C# в on line среда.

ПЛАН  НА  УРОКА:

В първите 15 минути  показвам и разяснявам как се използва On line среда на C#. За целта се използва  https://dotnetfiddle.net/ и

Web browser Google Chrome.

Запознаване с On line: Редактор, Дебъгер и създаване на конзолно приложение.

Език C# – начин за въвеждане и извеждане на информация (Пример):

В следващите 15 минути представям основни понятия и въведение в програмирането на C#:

C# e съвременен обектно-ориентиран език за програмиране от високо ниво с общо предназначение.

Ключови думи:

Оператори

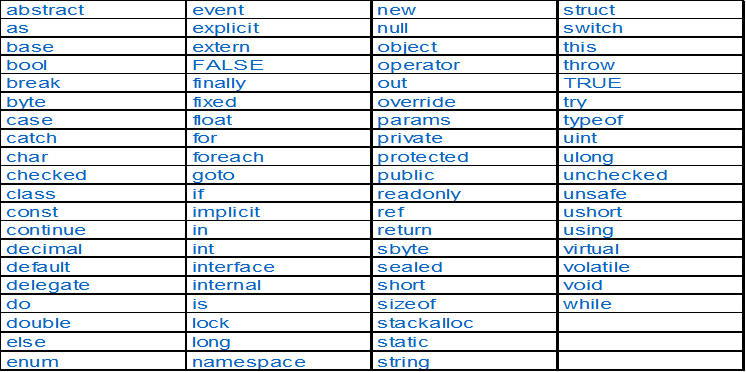
Във всички езици за програмиране се използват оператори, чрез които се извършват някакви действия върху данните. Нека разгледаме операторите в C# и да видим за какво служат и как се използват.

Операторите позволят обработка на прими­тивни типове данни и обекти. Те приемат като вход един или няколко операнда и връщат като резултат някаква стойност. Операторите в C# представляват специални символи (като например "+", ".", "^" и други) и извършат специфични преобра­зувания над един, два или три операнда. Пример за оператори в C# са знаците за събиране, изваждане, умножение и делене в математиката (+, - , *, /) и операциите, които те извършват върху целите и реалните числа.

Операторите в C#

Операторите в C# могат да бъдат разделени в няколко различни категории:

-        Аритметични – също както в математиката, служат за извършване на прости математически операции.

-        Оператори за присвояване – позволяват присвояването на стойност на променливите.

-        Оператори за сравнение – дават възможност за сравнение на два литерала и/или променливи.

-        Логически оператори – оператори за работа с булеви типове данни и булеви изрази.

-        По-битови оператори – използват се за извършване на операции върху двоичното представяне на числови данни.

-        Оператори за преобразуване на типовете – позволяват преобразу­ването на данни от един тип в друг.

Категории оператори:

Следва списък с операторите, разделени по категории:

Категория

Оператори

аритметични

-, +, *, /, %, ++, --

логически

&&, ||, !, ^

По битови

&, |, ^, ~, <<, >>

за сравнение

==, !=, >, <, >=, <=

за присвояване

=, +=, -=, *=, /=, %=, &=, |=, ^=, <<=, >>=

съединяване на символни низове

+

за работа с типове

(type), as, is, typeof, sizeof

други

., new, (), [], ?:, ??

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приоритет на операторите в C#

Някои оператори имат приоритет над други. Например, както е в математиката, умножението има приоритет пред събирането. Операторите с по-висок приоритет се изчисляват преди тези с по-нисък. Операторът () служи за промяна на приоритета на операторите и се изчислява пръв, също както в математиката.

В таблицата са показани приоритетите на операторите в C#:

Приоритет

Оператори

най-висок

 

 

 

 

 

...

 

 

 

 

 

най-нисък

++, -- (като постфикс), new, (type), typeof, sizeof

++, -- (като префикс), +, - (едноаргументни), !, ~

*, /, %

+ (свързване на низове)

+, -

<<, >>

<, >, <=, >=, is, as

==, !=

&, ^, |

&&

||

?:, ??

=, *=, /=, %=, +=, -=, <<=, >>=, &=, ^=, |=

 

Типове данни

Типовете данни представляват множества (диапазони) от стойности, които имат еднакви характеристики. Например типът byte задава множе­ството от цели числа в диапазона [0….255].

Характеристики

Типовете данни се характеризират с:

-     Име – например int;

-     Размер (колко памет заемат) – например 4 байта;

-     Стойност по подразбиране (default value) – например 0.

Видове

Базовите типове данни в C# се разделят на следните видове:

-     Целочислени типове – sbyte, byte, short, ushort, int, uint, long, ulong;

-     Реални типове с плаваща запетая – float, double;

-     Реални типове с десетична точност – decimal;

-     Булев тип – bool;

-     Символен тип – char;

-     Символен низ (стринг) – string;

-     Обектен тип – object.

Тези типове данни се наричат примитивни (built-in types), тъй като са вградени в езика C# на най-ниско ниво. В таблицата по-долу можем да видим изброените по-горе типове данни, техният обхват и стойностите им по подразбиране:

 

Тип данни

Стойност по подразбиране

Минимална стойност

Максимална стойност

sbyte

0

-128

127

byte

0

0

255

short

0

-32768

32767

ushort

0

0

65535

int

0

-2147483648

2147483647

uint

0u

0

4294967295

long

0L

-9223372036854775808

9223372036854775807

ulong

0u

0

18446744073709551615

float

0.0f

±1.5×10-45

±3.4×1038

double

0.0d

±5.0×10-324

±1.7×10308

decimal

0.0m

±1.0×10-28

±7.9×1028

boolean

false

Възможните стойности са две – true или false

char

'\u0000'

'\u0000'

‘\uffff’

object

null

-

-

string

null

-

-

 

Оператори за сравнение

В C# има няколко оператора за сравнение, които се използват за сравняване на двойки цели числа, числа с плаваща запетая, символи, низове и други типове данни:

Оператор

Действие

==

равно

!=

различно

> 

по-голямо

>=

по-голямо или равно

< 

по-малко

<=

по-малко или равно

 

В последните 15 минути представям:

 

Условна конструкция if else

В C#, както и в повечето езици за програмиране, съществува условна конструкция с else клауза: конструкцията if else. Нейният формат е, както следва:

if (булев израз)

{

      тяло на условната конструкция;

}

else

{

      тяло на else-конструкция;

}

 

Форматът на if else конструкцията включва: запазена дума if, булев израз, тяло на условната конструкция, запазена дума else, тяло на else конструкция. Тялото на else-конструкцията може да се състои от един или няколко оператора, заградени в къдрави скоби, също както тялото на условната конструкция.

Условна конструкция if else – пример

Нека разгледаме следния пример, за да покажем в действие как работи if else конструкцията:

static void Main()

{

      int x = 2;

      if (x > 3)

      {

            Console.WriteLine("x е по-голямо от 3");

      }

      else

      {

            Console.WriteLine("x не е по-голямо от 3");

      }

}

 

Програмният код може да бъде интерпретиран по следния начин: ако x>3, то резултатът на изхода е: "x е по-голямо от 3", иначе (else) резултатът е: "x не е по-голямо от 3". В случая, понеже x=2, след изчислението на булевия израз ще бъде изпълнен операторът от else конструкцията. Резултатът от примера е:

x не е по-голямо от 3

 

На следващата блок-схема е показан графично потокът на изчисленията от този пример:

clip_image003[4]

Давам за домашно: Да се състави алгоритъм и програма на C#, като от три въведени числа да се изведе текст и самото число, което е най-голямо.

 

УРОК 7

 

ТЕМА : Програмиране с оператори за цикъл на C#.

Вид на урока – комбиниран урок, в компютърен кабинет, продължителност 45 мин.

Опорни знания и умения

         До този урок са въведени и усвоени следните знания и умения, които имат отношение и ще бъдат използвани в урока:

·        Същност и видове алгоритми.

·        Съставяне различни видове блокови схеми на алгоритмите.

·        Представяне сорс код на С# в on line среда на интернет за въвеждане и извеждане на информация.

·        Ключови думи, Категории оператори, Типове данни на променливите.

·        Условен оператор If.

·        Съхраняване на данни в email и извеждането им.

·        Работа в Интернет среда с браузер.

Ресурсни материали:

Ø On line среда на C# : https://dotnetfiddle.net/

Цел на урока:

1.)  Упражняване съставяне на различни видове алгоритми.

2.)  Упражняване съставяне различни видове блокови схеми на алгоритмите.

3.)  Съставяне на сорс код на С# в on line среда на интернет на линейни, условни (разклонени) и циклични алгоритми.

Учебно съдържание:

Понятия:

-         Цикли в C#.

-         On line C#, Web browser, сорс код.

Умения за:

-         Познаване на циклични алгоритми, същност, свойства и видове.

-         Знания за съставяне на циклични алгоритми.

-         Реализация на знанията в съставяне на програма на C# в on line среда.

ПЛАН  НА  УРОКА:

Представям решението на домашното от миналия час:

представената програма се намира на адрес:

https://dotnetfiddle.net/gIFfW5#

Първите 15 минути за затвърждаване на знанията и усвояване на предадения учебен материал пускам следната презентация от адрес:

https://ucha.se/watch/3374/nashata-parva-csharp-programa

През следващите 15 минути представям цикли в C#, както следва:

ЦИКЪЛ е основна конструкция в програмирането, която позволява многократно изпълнение на даден сорс код. В зависимост от вида на цикъла, кода в него се повтаря фиксиран брой пъти или докато е в сила дадено условие

Видове цикли в C#: while, do-white, For, foreach, вложени.

Ще разгледаме само първите три, като по-разпространени в практиката:

Конструкция за цикъл while

Един от най-простите и най-често използвани цикли е while.

while (условие)

{

          тяло на цикъла;

}

В кода по-горе условие представлява произволен израз, който връща булев резултат – истина (true) или лъжа (false). Той определя докога ще се изпълнява тялото на цикъла и се нарича условие на цикъла (loopcondition). В примера тяло на цикъла е програмният код, изпълняван при всяко повторение (итерация) на цикъла, т.е. всеки път, когато входното условие е истина. Логически поведението на while циклите може да се опише чрез следната схема:

clip_image001

При while цикъла първоначално се изчислява булевият израз и ако ре­зултатът от него е true, се изпълнява последователността от операции в тялото на цикъла. След това входното условие отново се проверява и ако е истина, отново се изпълнява тялото на цикъла. Всичко това се повтаря отново и отново докато в някакъв момент условният израз върне стойност false. В този момент цикълът приключва своята работа и програмата продължава от следващия ред веднага след тялото на цикъла.

Понеже условието на while цикъла се намира в неговото начало, той често се нарича цикъл с предусловие (pre-test loop). Тялото на while цикъл може и да не се изпълни нито веднъж, ако в самото начало е нарушено условието на цикъла. Ако условието на цикъла никога не бъде нарушено, той ще се изпълнява безкрайно.

Пример:

Сумиране на числата от 1 до N – пример

В настоящия пример ще разгледаме как с помощта на цикъл while можем да намерим сумата на числата от 1до n. Числото n се чете от конзолата:

Console.Write("n = ");

int n = int.Parse(Console.ReadLine());

int num = 1;

int sum = 1;

Console.Write("The sum 1");

while (num < n)

{

            num++;

            sum += num;

            Console.Write(" + " + num);

}

Console.WriteLine(" = " + sum);

Първоначално инициализираме променливите num и sum със стойност 1. В num пазим текущото число, което добавяме към сумата на предходните. При всяко преминаване през цикъла увеличаваме num с 1, за да получим следващото число, след което в условието на цикъла проверя­ваме дали то е в интервала от 1 до n. Променливата sum съдържа сумата на числата от 1 до num във всеки един момент. При влизане в цикъла добавяме към нея поредното число записано в num. На конзолата принти­раме всички числа num от 1 до n с разделител "+" и крайния резултат от сумирането след приключване на цикъла. Изходът от програмата е следният (въвеждаме n=17):

n = 17

The sum 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 = 153

 

Конструкция за цикъл do while

Do while цикълът е аналогичен на while цикъла, само че при него проверката на булевото условие се извършва след изпълнението на операциите в цикъла. Този тип цикли се наричат цикли с условие в края (post-test loop). Един do while цикъл изглежда по следния начин:

Do

{

          код за изпълнение;

}

while (израз);

Схематично do while циклите се изпълняват по следната логическа схема:

clip_image003

Първоначално се изпълнява тялото на цикъла. След това се проверява неговото условие. Ако то е истина, тялото на цикъла се повтаря, а в противен случай цикълът завършва. Тази логика се повтаря докато условието на цикъла бъде нарушено. Тялото на цикъла се повтаря най-малко един път. Ако условието на цикъла постоянно е истина, цикълът никога няма да завърши.

Използване на do while цикли

Do-while цикълът се използва, когато искаме да си гарантираме, че поредицата от операции в него ще бъде изпълнена многократно и задължително поне веднъж в началото на цикъла.

Пример:

Изчисляване на факториел – пример

В този пример отново ще изчислим факториела на дадено число n, но този път вместо безкраен while цикъл, ще използваме do while. Логиката е аналогична на тази в предходния пример:

Console.Write("n = ");

int n = int.Parse(Console.ReadLine());

decimal factorial = 1;

do

{

          factorial *= n;

          n--;

} while (n > 0);

Console.WriteLine("n! = " + factorial);

Започваме в началото от резултат 1 и умножаваме последователно на всяка итерация резултата с n и намаляваме n с единица докато n достигне 0. Така получаваме произведението n*(n-1)*…*1. Накрая отпечатваме получения резултат на конзолата. Този алгоритъм винаги извършва поне 1 умножение и затова няма да работи коректно при n=0, но ще работи правилно за n ≥ 1.

Ето го и резултатът от изпълнение на горния пример при n=7:

n = 7

n! = 5040

В оставащите последни 15 минути представям:

Конструкция за цикъл for

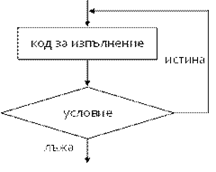
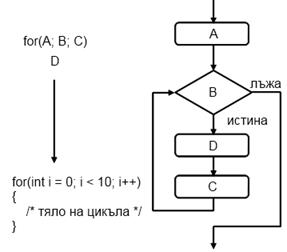
For циклите са малко по-сложни от while и do while циклите, но за сметка на това могат да решават по-сложни задачи с по-малко код. Ето как изглежда логическата схема, по която се изпълняват for-циклите:

clip_image010

Те съдържат инициализационен блок (A), условие на цикъла (B), тяло на цикъла (D) и команди за обновяване на водещите променливи (C). 

For цикъл – примери

Ето един цялостен пример за for-цикъл:

for (int i = 0; i <= 10; i++)

{

          Console.Write(i + " ");

}

 

Резултатът от изпълнението му е следният:

0 1 2 3 4 5 6 7 8 9 10

 

Ето още един по-сложен пример за for цикъл, в който имаме две водещи променливи i и sum, които първоначално имат стойност 1, но ги обновя­ваме последователно след всяка итерация на цикъла:

for (int i = 1, sum = 1; i <= 128; i = i * 2, sum += i)

{

          Console.WriteLine("i={0}, sum={1}", i, sum);

}

 

Резултатът от изпълнението на цикъла е следният:

i=1, sum=1

i=2, sum=3

i=4, sum=7

i=8, sum=15

i=16, sum=31

i=32, sum=63

i=64, sum=127

i=128, sum=255